What will happen to future interest rates? Will they fall back to pre-pandemic lows, will they stay more or less at current levels or will they rise? Many people say: “Just see what the market expects”. So let’s do that. The market expects interest rates in the future to stay roughly where they are now. But is that a good prediction?
In previous analyses, I have discussed the long-term outlook for interest rates, for instance in my analyses of r* (link). Such analyses often conclude that interest rates are likely to be relatively low in the future. Such predictions, though, depend on the specific models used to back out r* and the assumptions made when applying the models.
As an alternative, one sometimes hears comments like: “Why make it so complicated? Why not simply look at what the markets expect?”
Let’s do that. Let us look at the implied future interest rates – or forward rates – that can be derived from current interest rates of different maturities.
Market-implied forward interest rates as predictors of future interest rates differ fundamentally from forecasts based on models of equilibrium interest rates such as r*. The latter usually have a sound theoretical basis, but do not necessarily reflect what investors expect. The former may reflect what investors expect, but may not be consistent with theoretical models of how the economy works.
Market-implied forward rates
Market-implied forward interest rates are derived from current interest rates of different maturities. If a one-year interest rate today is 4% and a two-year interest rate today is 5%, this tells us that the implied one-year forward interest rate (one-year interest one year from now) is:
F(1,1) = [(1 + 5%)^2/(1 + 4%)^1]^(1/(2-1)) = 6%
Many argue that this should be the market’s best estimate of the one-year interest rate in one year. The idea is that the return you get from buying a two-year bond should be the same as the return you would expect if you buy a one-year bond today and a one-year bond in a year’s time.
You know what the yield on the one-year bond is today – you can see that in the market. Together with today’s yield on the two-year bond, this gives you what investors expect the one-year yield to be in one year’s time. This is also known as the “expectation theory of interest rates”.
We can perform this type of calculation for bonds with different maturities. For example, if we use the yield on a ten-year bond today together with the yield on a twenty-year bond today, we can calculate what investors implicitly expect the ten-year interest rate to be in ten years’ time, i.e. the ten-year forward interest rate in ten years’ time. The formula for this calculation is:
F(10,10) = [(1 + i(0,20))^20/(1 + i(0,10))^10]^(1/(20-10))
In this expression, i(0,10) and i(0,20) are the ten- and twenty-year interest rates today.
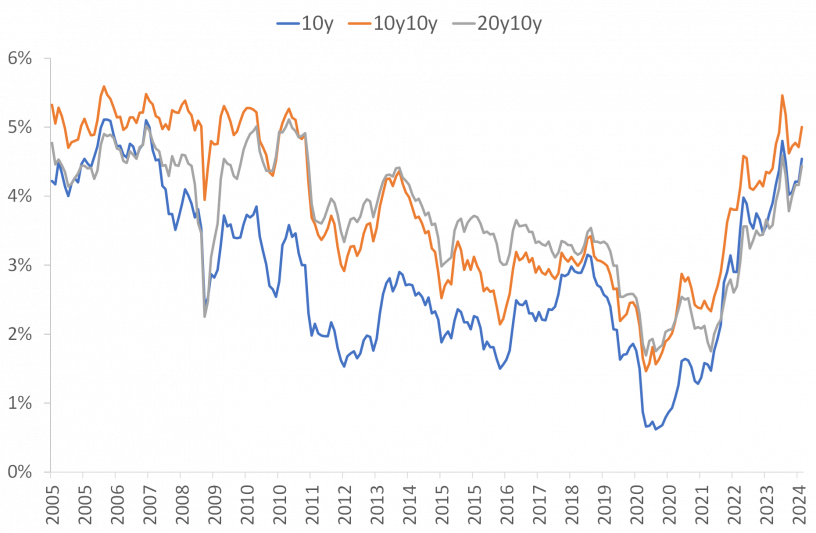
Figure 1 shows the development of the yield on ten-year US Treasuries (labelled 10y in the chart) over the last two decades, the market-implied ten-year forward rate in ten years (10y10y) and the market-implied ten-year forward rate in twenty years (20y10y).
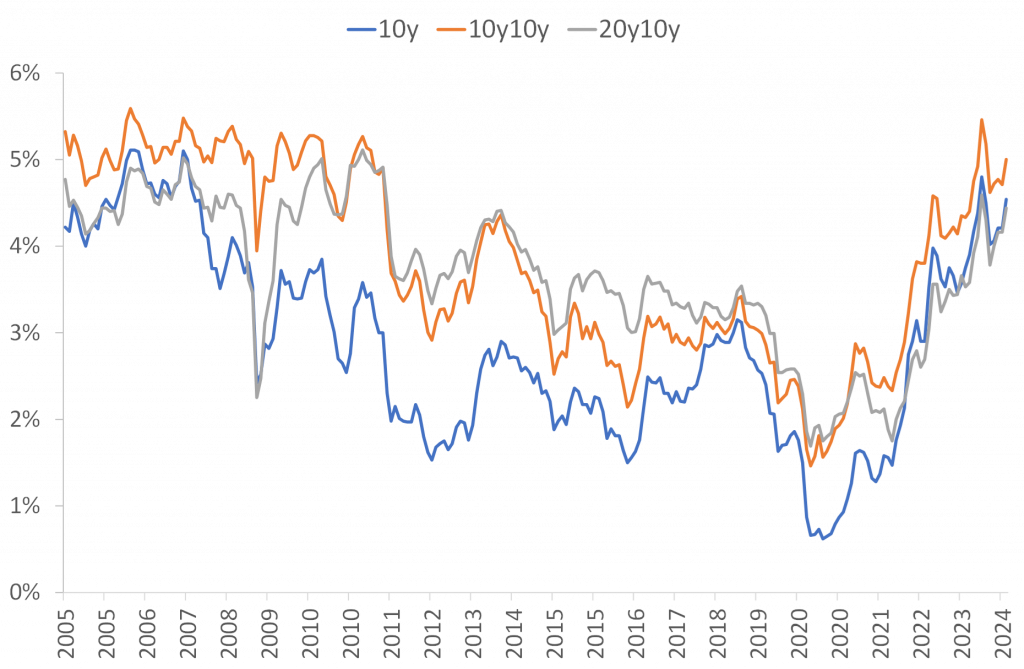
Figure 1. Yield on ten-year Treasuries, ten-year forward rates in ten years (10y10y) and ten-year forward rates in twenty years (20y10y). 2005-2024. Data source: St. Louis FRED and J. Rangvid.
Figure 1 leads to two general conclusions. First, the forward interest rates implied by the market follow the movements of current interest rates: When current interest rates fall, forward rates also fall and vice versa.
Secondly, although forward rates follow current rates, they are usually slightly higher than current rates. For example, the current 10-year US interest rate is 4.5%, but the market-implied 10-year forward rate in ten years is 0.25% percentage points higher.
Since 10y, 10y10y and 20y10y are more or less the same now (though 10y10y is slightly higher than 10y), this means that using forward interest rates as predictors of future interest rates leads to the conclusion that the market does not expect interest rates to fall or rise significantly from current levels. For example, investors do not expect interest rates to return to pre-pandemic lows. Ten-year interest rates are at 4.5% today and the market expects ten-year interest rates to be more or less the same in ten years’ time and also more or less the same in twenty years’ time.
Are market-based measures of expectations good measures of future outcomes?
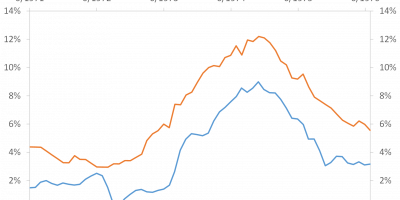
The fact that market-implied forward rates follow current interest rates already indicates that they are not necessarily good predictions of future realised interest rates. When a temporary shock pushes up current interest rates, market-based expectations tend to follow suit. But if it really is a temporary shock, then future interest rates should not be affected. This is perhaps clearest to see if we go back even further, i.e. to the early 1950s, for which we have data on 20-year Treasuries, such that we can calculate 10y10y forward rates. From 1977, we have 30-year Treasuries allowing us to calculate 20y10y forward rates. These are shown in Figure 2.
Figure 2 again illustrates the strong correlation between current interest rates and market-implied forward rates, but now for a long period of time that includes both the period when interest rates were rising, i.e. the 1960s and 1970s, and the period when interest rates were falling, i.e. the last four decades.
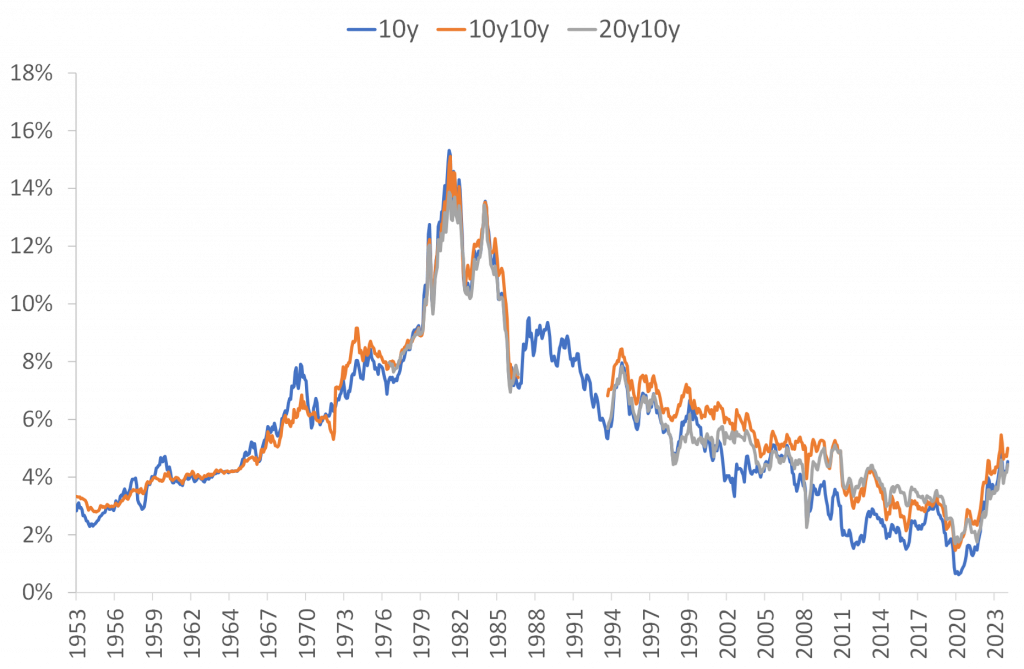
Figure 2. Yield on ten-year Treasuries, ten-year forward rates in ten years (10y10y) and ten-year forward rates in twenty years (20y10y). 1953-2024. Data source: St. Louis FRED and J. Rangvid.
When interest rates peaked at 15% in the early 1980s, so did market-implied forward rates. Assuming that forward interest rates are good estimates of future interest rates, this means that in 1982, when interest rates peaked, investors expected interest rates to be the same in ten years, i.e. 1992, as they were in 1982. More specifically, this meant that in 1982, investors expected the ten-year interest rate to be 15% in 1992. Instead, interest rates in 1992 had fallen by around eight percentage points to 7%.
The situation was similar in a period of rising interest rates. In the early 1970s, when interest rates were at 6%, investors expected that ten years later, in the early 1980s, interest rates would also be 6%. Instead, interest rates in the early 1980s rose by almost ten percentage points compared to the level of the early 1970s. Market-based expectations are often wrong.
The idea that forward interest rates measure expected future shorter interest rates is based on the so-called “expectations theory of interest rates”. It has been extensively tested in the academic literature. Often, it is rejected, see for instance classic studies by Fama (1984), Fama and Bliss (1987), Campbell and Shiller (1991), and Bekaert and Hodrick (2001).
Conclusion
There is a high correlation between current interest rates and expected interest rates as implied by market-implied forward rates. As the US ten-year interest rate today is around 4.5%, this means that these models predict that the US ten-year interest rate will also be around 4.5% in 2034 and 2044. Academic research has found that such expectations are usually not good predictions of future outcomes. An alternative could be to look at expectations based on sound economic modelling, such as estimates of future r*, as discussed in previous analyses (link). These estimates suggest that future interest rates will be low.