Category: Oil
Page 1/1

Inflation expectations, Oil, Uncategorized
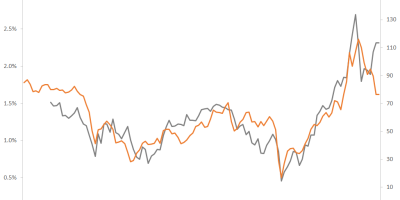
Oil prices and inflation expectations

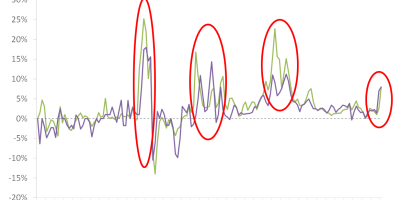
Did energy prices cause this inflation surge?

Eurozone, Inflation, Monetary policy, Oil
ECB’s additional dilemma
Inflation, Monetary policy, Oil
Is 1970s-like inflation coming back?
Corona crisis, Oil, Stock markets